numbers

types of numbers

People like to sort and classify. Maybe you collect rocks or stamps or pokemon cards. And maybe you try to sort them. Maybe by color or by the numbers on it or by their size. Well, mathematicians are not different. They like to sort their nuumbers too and so we come to different types of numbers.

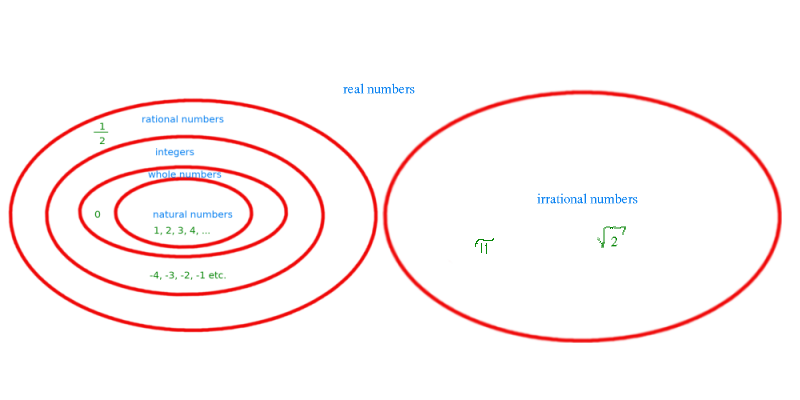
The smallest set of numbers in our classification are the natural numbers. These are the numbers we first come in contact with when we learn to count. We first learn the natural numbers like 1,2,3.

Then at one point the 0 is added, after all it is possible that there is 0 of something and we get the whole numbers. Whole numbers are the natural numbers including zero.

Soon we learn that this still is not enough. Think about a cold winter's day when the temperatures go below zero. Or if you owe money to someone. We also need negative numbers. Put all of them together and we get the integers.

It seems like we now have included a lot of numbers. But well, what is for example between 1 and 2? Or between 533 and 534? Well, a whole lot of numbers it turns out. The rational numbers include all the numbers that we have seen before plus fractions. Examples of fractions are 1/2 or 4/5. A fraction has a nominator and a denominator. The nominator is the number at the top of the fraction and the denominator is the number at the bottom. It's easy to remember. Something is more stable if it is wider at the bottom and the word denominator is longer/wider than the word nominator.
In rational numbers the denominator cannot be zero.
Are these now all the numbers that we know in the universe? No, actually not. There are also irrational numbers. An example of an irrational numbers is the square root of 2. You see the fractions from the rational numbers? You can also express them as decimal numbers. But it turns out that there are decimal numbers like the square root of 2 that cannot be expressed as a fraction. And these are called irrational numbers. Pi is another example of an irrational number. It is used in calculating circles. And even though both sets, the set of rational numbers and the set of irrational numbers are infinitive but still the set with the irrational numbers is bigger (look for infinity, Cantor and diagonal proof to get further into this).

If you put the rational and the irrational numbers together we get the real numbers and this is really the complete set of numbers that we know about...