multiplication trick for 2 numbers between 6 and 9

multiplication trick for 2 numbers between 6 and 9

It's fun to do multiplication with your fingers. So I was delighted when I came across this multiplication finger trick for multiplying 2 numbers between 6 and 10 on the mathandmultimedia.com webpage. Here's how it's done:

First you put your hands next to each other with the fingers facing each other (like in the picture). Number your fingers from 6 to 10, starting with 6 at the bottom and ending with 10 at the top.

finger math

Align your fingers such that the fingers with the numbers you want to multiply directly face each other. Let's take 8*7 as our example.

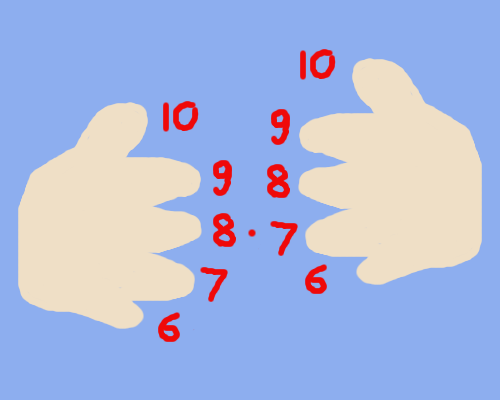
finger math

Next we count the fingers that face each other as well as all the fingers below in steps of ten.
In our example of 8*7 we count 10+10+10 = 30 on the left hand and 10+10=20 on the right hand. Together this is 30+20=50. (step1)

Now you count the remaining fingers (the fingers on top of the fingers that face each other) of the left hand and multiply that number with the number of the remaining fingers of the right hand.
In our example that is 3*2=6. (step2)

To get the result of the multiplication you wanted to calculate you add the two results you got together, that is in our example 50+6=56. (step3)

Let's try it for 7*7:

finger math

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 20+20=40.
For the fingers on top you get 3*3 = 9
Add the two results together and you get 49.

Let's try 8*8:

finger math

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 30+30=60.
For the fingers on top you get 2*2 = 4
Add the two results together and you get 64.

Let's try 7*9:

finger math

Aligning your fingers and then counting the fingers that are facing each other plus the ones below in steps of ten you get 20+40=60.
For the fingers on top you get 3*1 = 3
Add the two results together and you get 63.

You can see that the method is working by looking at the algebra behind it.

Let's call our two numbers x and y, that is we want to solve x*y.
Let's try to express what we did with our hands in algebraic form.
We first count the fingers on one of our hands from 6 to x. That is the same as writing x-5.
(I hope you can see that it is the same. We need to subtract 5 as we don't count from 1 but from 6 only)
We do the same with the other hand and get y-5.
We actually counted in steps of 10 which is the same as multiplying our result by 10. So we can write 10*(x-5) + 10*(y-5) (step1)
(or 10*((x-5) + (y-5)) which by using the distributive law a*(b+c) = a*b + a*c is the same).

Next we counted the fingers from our number to 10 on each hand and multiplied them with each other.
To get to this number we can write 10-x and 10-y respectively.
(Think about what we did, we counted from our number up to 10 which is the same as finding the difference between 10 and our number, or subtracting our number from 10)
Next we multplied the counted numbers:
(10-x)*(10-y) (step 2)

To get the result we are looking for we then needed to add our 2 results together (step3):
10*(x-5) + 10*(y-5) (from step1) + (10-x)*(10-y) (from step 2)
Now we only need to simplify this expression a bit:
10*(x-5) + 10*(y-5) + (10-x)*(10-y) <==>
10x -50 +10y -50 +100 -10y -10x +xy <==>
100 - 50 -50 + 10x - 10x + 10y - 10y + xy <==>
xy

q.e.d. (quod erat demonstrandum = what was to be shown)

references

http://mathandmultimedia.com/2011/04/23/finger-math-multiplication

http://mathandmultimedia.com/2011/05/12/why-finger-multiplication-works